Highest Mountains (according to standard view)
| Asia | Qomolangma Feng | 8848m |
| South America | Aconcagua | 6959m |
| North America | Mt. McKinley | 6193m |
| Africa | Kibo | 5895m |
| Europe | Elbruz | 5642m |
| Antartica | Vinson Massif | 5140m |
| Australia & Oceania | Punjak Jaya | 5030m |
The absolute height of a mountain *
By Karl G.B. Wendekreis
**
We define the absolute height of a mountain as its relative height, which is the height which appears in most reference works, plus the distance to the centre of the earth.
To determine the absolute height, we need some standard geometrical formulae.
Eq. 4 ![]()
Figure 1 gives a graphical explanation of the used equations.
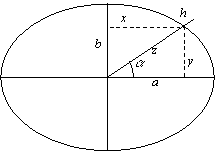
Figure
1. Graphical representation of key parameters.
As the distance from the poles to the centre of the earth is smaller than the distance from the equator to the centre of the earth, one can expect mountains with a small latitude (situated close to the equator) to have a large absolute height.
It is straigthforward that the absolute height can be calculated by combining the well-known eleptoic earth constants together with the latitude and the relative height.
This will be shown by comparing the absolute height of Quomolangma Feng with some mountains situated close to the equator. The necessary data are presented in Table 1 and Table 2.
| Name | Country | Height (standard view) |
Latitude |
| Quomolangma Feng | China/Nepal | 8848m | 28°, N |
| Nev. de Huascarán | Equador | 6768m | 9°, S |
| Chimborazo | Equador | 6310m | 2°, S |
| Cayambe | Peru | 5790m | 0°, S |
Table
1. Relative height and latitude of key mountains.
| Distance to the equator (a) |
6378137m |
| Distance to the poles (b) |
6356752m |
Table
2. Ellipsoid Constants (GRS-1980).
The derivation is not left as an exercise to the reader.
| Eq. 3 | Eq. 5 | ||
| Eq. 2 | Eq. 6 | ||
| Eq. 5, Eq. 6 | |||
| Eq. 7 | |||
| Eq. 6, Eq. 7 | Eq. 8 | ||
| Eq. 4, Eq. 8 | |||
| Eq. 9 | |||
| Eq. 1, Eq. 9 | Eq. 10 |
By applying Eq. 10 to the given data, the results *** become apparent (Table 3). It is evident that the absolute heighest mountain on earth is the Chimborazo.
| Name |
h |
z |
|h| |
| Chimborazo | 6310m | 6378110m | 6384420m |
| Nev. de Huascarán | 6768m | 6377611m | 6384379m |
| Cayambe | 5790m | 6378137m | 6383927m |
| Quomolangma Feng | 8848m | 6373405m | 6382253m |
Table
3. Absolute height of key mountains.
* An extented version of this paper is published in the Journal of Derived Mathematics, Is. Jan. 1999.
** Doctor Karl G.B. Wendekreis is lector at the Elbruz Science Institute in Chamonix (Fr.). He publishes on various mathematical subjects.
*** The calculations were made on a multi-processor Cytrix-306. The FORTRAN program lasted 17 hours.